编译原理学习记录

1 引论

背书.GIF

2 编译基础知识

2.1 高级语言

程序语言是一个记号系统。
语言=语法+语义

2.2 语法

语法：使得字符形成一个形式上正确的程序
语法=词法规则 + 语法规则

2.2.1 单词符号

单词符号：语言中具有独立意义的基本结构

一般来说有：常数，标识符，基本字，算符，界限符

词法规则：规定字母表哪些字符串是单词符号
可以使用正规式和有限自动机来描述词法结构和进行词法分析

2.2.2 语法单位

语法单位：表达式，子句，语句，函数，过程，程序

语法规则：规定了如何从单词符号来形成语法单位

语言的词法规则和语法规则定义了程序的形式结构，是判断输入字符是否构成一个形式上正确的程序的依据。

2.3 字母表和符号串

2.3.1 概念

1. 字母表：非空有穷集合；用Σ和V表示
2. 符号：是语言中最基本的不可再分的单位
3. 符号串：空串ξ
4. 句子：字母表上符合某种规则构成的串
5. 语言：句子的集合

习惯：a,b,c,…表示符号；α,β,υ,…表示符号串；A,B,C,…表示集合。

2.3.2 符号串的集合

1. 连接（乘积）运算：类似笛卡尔积，若A={α₁,α₂,α₃,…},B={β₁,β₂,β₃,…},则AB={αβ|α∈A且β∈B}

• 串集自身的乘积称作串集的方幂
• A⁰={ξ}
• 字母表A的n次幂是字母表A上所有长度为n的串集
• 乘积有顺序的A={a,b};B={c,e,d},则AB={ac,ad,ae,bc,bd,be} ac的顺序不可调换
  
  

1. 字母表的闭包 A^*= A⁰ ⋃ A¹ ⋃ A² ⋃ …
   即由A上符号组成的所有穿的集合，包括空串ξ
   
   字母表的正闭包 A⁺= A^* - {ξ}

字母表上的语言是字母表上正闭包的子集

2.4 文法与语言

2.4.1 文法的概念

文法是描述语言的语法结构的形式规则

1. 非终结符：出现在规则左部；大写字母或用<>括起来，表示一定语法概念的词；用 V_N表示
2. 终结符：语言中不可分割的字符串，是组成句子的基本单位；用V_T表示。
3. 开始符号：又称识别符号，所定义语法范畴的非终结符
4. 产生式：形式 A → α，A产生α
5. 推导：事实上，你替换任何一个都可以…
   最左（右）推导：
   每次使用一个规则，以其右部取代符号串最左（右）非终结符
   都为规范推导
6. 归约：归约是推导的逆过程，最左（右）归约是最右（左）推导的逆过程
   都为规范归约
   若某个父亲节点的所有孩子都为叶子节点时才能归约
7. 句型、句子和语言

• 句型：
• 句子：
• 语言：

1. 语法扩充：BNF、元语言符号（指路第一章）

2.4.2 文法与语言的形式定义

1. Chomsky的定义：G(V_N,V_T,P,S)
2. Chomsky的分类：

• 0型文法：（短语文法或无限制文法）P中产生式α→β,α∈V⁺并至少含有1个非终结符，β∈V^*
  识别0型文法的自动机为图灵机；产生式限制最少，可枚举，可递归
• 1型文法：定义看书P25;
  （上下文有关、长度增加文法）
  识别1型文法的自动机为线性界限自动机；理解定义：非终结符替换必须在某个特定的上下文中且不可替换为ξ，除非是S→ξ
• 2型文法：上下文无关
  识别1型文法的自动机为下推自动机（PDA）是判断句子是否正确的标准
• 3型文法：正规文法，非终结符全在最右边右线性文法or最左边左线性文法or没有）
  识别3型文法的自动机为有限状态自动机
  是判断单词是否正确的标准

  上下文无关文法包含了正规文法

1. 文法分类的具象表现

• 0型文法　 α→β
• 1型文法 　αAβ→αυβ
• 2型文法　 A→α（任意符号串）
• 3型文法　 A→Bα|α
  　　　　　A→αB|α

1. 文法化简的步骤
2. 构造无ξ产生式的上下文无关文法的条件 (ξ规则)

• P中要么不含有ξ产生式，要么只有S→ξ
• 若S→ξ，则S不出现在任何产生式的右部

2.5 语法树与文法的二义性

2.5.1 语法树

1. 定义：用来表示语言句子结构的树
2. 作用：易于判断文法二义性

2.5.2 语法树的一些概念

1. 句型：在一棵语法树生长过程中的任何时刻，所有那些叶子节点排列起来就是一个句型
2. 短语：子树的末端符号自左向右连成串，相对于子树树根而言称为短语
   简单短语（直接短语）：若短语是某子树根进过一步推导得到的
3. 句柄：句型中的最左简单短语；句柄是最左归约时要寻找的简单短语

2.5.3 文法的二义性

1. 句子二义性：若一个句子存在对应的两棵或两棵以上的语法树，则句子是二义的
2. 文法二义性：有句子二义性的文法

3 词法分析

3.1 正则表达式（正规式）

用来描述正则语言更紧凑的表示方法

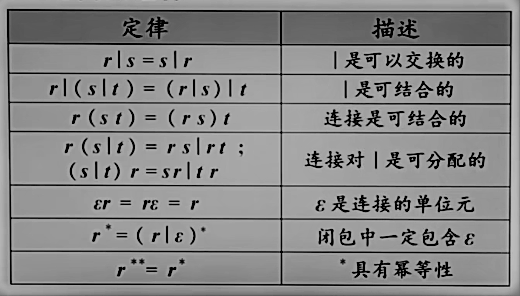
1. 定义：正则表达式可以由较小的正则表达式按照特定规则递归地构建。每个正则表达式r定义一个语言L(r)
2. 若r,s都是RE
   r|s是RE, L(r|s)=L(r) ⋃ L(s)
   rs是RE, L(rs)=L(r)L(s)
   r^* 是RE, L(r^* )=(L(r))^*
   (r)是RE, L((r))=L(r)
   运算优先级：() → * → 连接 → |

1. RE的代数定律
   
   

   3.2 正则定义

   给一些RE命名， 并在之后的RE中像使用字母表中的符号一样使用这些名字

3.3 有穷自动机(FA)

经典例子：电梯控制装置

3.3.1 转换图（Transition Graph）

• 结点：FA的状态
  初始状态(开始状态)：只有一个，由start箭头指向
  终止状态(接收状态)：可以有多个，用双圈表示
• 带标记的有向边：边上标记为输入

3.3.2 FA定义(接收)的语言

输入串能让有穷状态机从初始状态转换到终止状态，该串被接收。

所有可接收串构成的集合为FA定义（或接收）的语言，记为L(M)

3.3.3 有穷自动机的分类

1. 确定的FA(Deterministic finite automata, DFA)

• 定义为五元组 M=(K,Σ,f,S,Z),书P48
• DFA即可以用转换图表示，也可以用转换表表示

1. 非确实的FA(Nondeterministic finite automata, NFA)

• 与DFA的唯一区别：沿着标记能到达的状态不唯一
• NFA的边上还能标记ξ, 带有“ξ-边”的NFA

  带有“ξ-边”的NFA与不带“ξ-边”的NFA等价
  DFA与NFA具有等价性
  
  DFA与RE也等价
  
  四者相互等价

1. DFA与NFA比较

• DFA计算机更好实现
• NFA更加直观

1. DFA的算法实现

   K=S；
   c=getchar();//当前输入符号
   while (c<>eof()) 
   {K=f(K,c);
   c=getchar();
   }
   if (K in Z) return (“yes”)//遇到文件结束符号
   else return (“no”)

   3.3.4 从正则表达式到有穷自动机

2. 从RE到NFA

• 套用下面

1. 从NFA到DFA

<font size='3' color='#6495ED'></font>
<font size='3' color='#DC143C'></font>